Diffie-Hellman 算法简单应用

只是简单介绍，并未深入研究。

Diffie-Hellman 是一种密钥交换协议，不用于加密，而是在双方提前没有进行任何通讯并且所有通讯都公开的情况下交换密钥。 可以为后续加密传输做准备。

Diffie-Hellman 简介Permalink

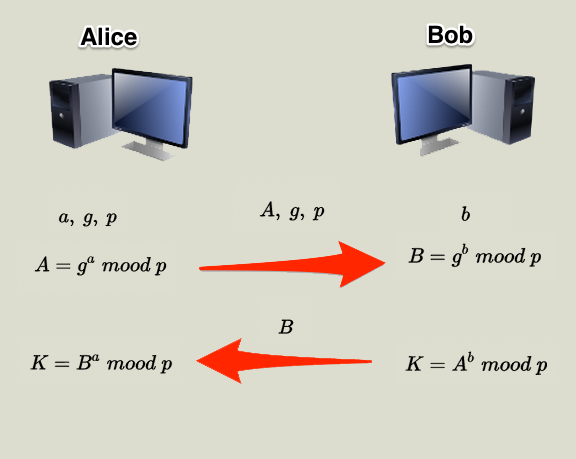
Alice和Bob计算出的K是相同的，由下面公式简单推导可得：

除了 a 和 b 以外，其他数据都是公开的。Alice 无需知道 Bob 的 b 是多少，所以 a 和 b 不需要传输，从而保证了安全。 要强调的是 p 必须足够大才能保证安全性，如果 p=5 那对 p 求模运算之后无非五种可能： (0,1,2,3,4) 直接试验就可以攻破了。 而 g 则不需要很大。

安全性分析Permalink

该算法的安全性基于有限域上求解离散对数非常困难。参见三大数学难题中的离散对数问题。

但其本身是一个无认证的密钥交换协议。所以还是存在中间人攻击(Man-in-the-middle attack, MITM)。

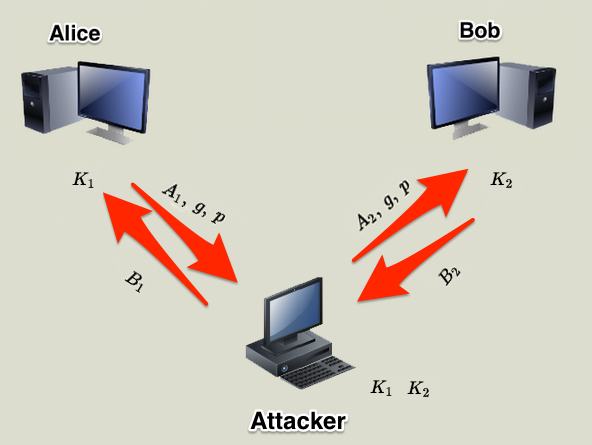
Attacker 截获 Alice 传给 Bob 的 A,g,p，并伪造相应数据发送给 Bob，同时模拟 Bob 返回给 Alice 计算结果。 也就是说进行了两次 Diffie-Hellman 密钥交换过程。Alice 和 Attacker 之间有相同的密钥 K1，Attacker 和 Bob 之间有相同的密钥 K2。

攻击者必须进行实时监控和转发，否则立刻就会被发现。

应用Permalink

• Secure Socket Layer (SSL)
• Transport Layer Security (TLS)
• Secure Shell (SSH)
• VPN

应用于远程文件的校验Permalink

储存在远程主机上文件的安全性非常重要，这里只讨论不经常修改重要文件，如 /boot，/etc/passwd 等文件。

文件完整性检检查一般是用签名等方法，但安全系数不高。

基于 Diffie-Hellman 算法进行改进之后可以用于检测远程文件的完整性。

• m：待检测文件
• N：大素数，同 Diffie-Hellman 中的 p，可公开
• a：任意整数，同 Diffie-Hellman中的 g，可公开

1. 将文件递交到远程服务器之前先计算 M=am mod N，本地保存 M 值
2. 产生随机数 r，计算 A=ar mod N，将校验请求和A值发送给远程服务器
3. 远程服务器收到请求后计算 B=Am mod N，将结果返回给本地服务器
4. 本地服务器计算 C=Mr mod N，并比较 C 与 B 是否相等，若相等说明文件完整，未被修改

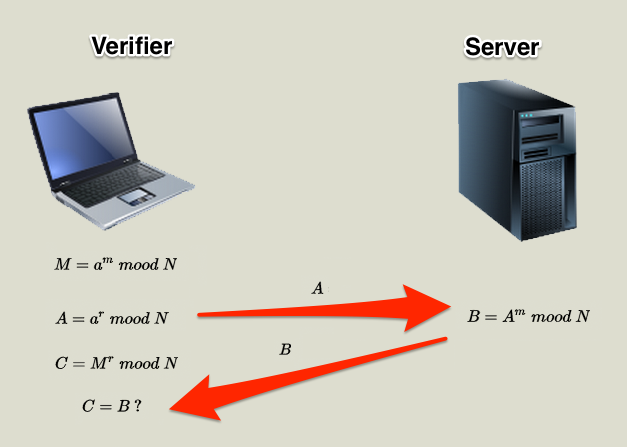
由上面公式可知，若 C=B，说明 m 未被修改。 但是由于 Diffie-Hellman 算法本身无法抵制中间人攻击，攻击者可以在删改文件之前备份，然后截获检验请求，即可绕过检验。 所以在在验证远程文件安全性之前需要确认服务器身份。 例如添加在Server返回计算结果 B 的同时要求携带身份认证信息，Verifier 接收到返回结果时，先进行确认身份是 Server 之后再检验 B 和 C 是否相等。

才疏学浅，若有不当，敬请指正。